Lord Kelvin Biography

[Repubished from Cassier’s Magazine from the original article by
By J.D. Cormack, B.Sc., M.I.E.E. published 1899.]

AT the close of a century, unequalled in the history of the world for progress in civilisation and science, looking backward, and tracing the growth of old, the beginning and development of new sciences and the close union of theory and practice which has proved so productive of benefit to mankind, we see prominently everywhere and at every stage the work of one universal genius, — William Thomson, afterwards Sir William Thomson, and now Lord Kelvin.

For fifty-three years, as professor of natural philosophy at the University of Glasgow, he has explained in his introductory lecture that natural philosophy has for its aim the observation and classification of the operations of nature, and the discovery of its laws by inductive generalisation based upon these observations. Taking this wide view of the subject which he was called upon to teach, he has, for nearly sixty years, striven earnestly, patiently, incessantly and successfully to extend our knowledge of nature, and to apply it in the service of man. Mathematics, mechanics, sound, light, heat, thermodynamics, magnetism, electricity, elasticity, telegraphy, electrical engineering, geology, astronomy, chemistry, and navigation are all indebted to him. His genius, profound and prolific, makes him one of the most remarkable men in a remarkable age.

A glance at the parentage and early training of one who has secured a niche in the temple of fame cannot fail to be interesting. Lord Kelvin’s father, James Thomson, a descendant of a Scottish farming family, settlers in Ulster, was born near Ballynahinch, County Down. He early displayed powers of observation and reasoning, and, as a boy, took up the study of mathematics in order to master the difficulties he had encountered in understanding the principles of dialling. Encouraged in his studies by his father, he attended a small classical and mathematical school in the neighbourhood, and there he made such progress that he was promoted to be assistant teacher. The Scottish University system provided then, even more effectively than it does now, a university education at a cost within the reach of men of very slender means, and of this James Thomson took advantage, studying at Glasgow in winter and teaching at home in summer.

After five years thus spent, during which he evinced thorough scholarship, wide sympathies and special devotion to mathematics, he was appointed headmaster of the school of arithmetic and geography at the Royal Academical Institution, Belfast, being afterwards promoted to the professorship of mathematics there. In Belfast he married, and had a family of five sons and three daughters. William was born on June 25, 1824, and was two years younger than his brother James, who, afterwards, as professor of civil engineering and mechanics, became his colleague in the University of Glasgow.

In 1832, when William was eight years old, the Thomsons removed to Glasgow. The father had been appointed to the professorship of mathematics in the university where he had been a student, and entered on duties which he continued to discharge till his death, in 1849. He is still remembered as a man of wide culture and thorough scholarship, an enthusiastic, and eminently successful teacher, the author of many important memoirs, and of a series of mathematical text-books, unsurpassed for method of treatment and lucidity of style.

William, with his brothers and sisters, received his early education from the father. At the age of ten he went to school, and a year later entered the university with his brother James. He soon distinguished himself, gaining, among other honours, the first prizes in the junior and senior mathematical classes, and winning, in 1838, a “University Prize” for an essay on “The Figure of the Earth.” Fascinated though he was by the study of mathematical science, he did not pursue it to the neglect of classics and mental philosophy. He embraced to the full the advantages of a liberal education, and to-day laments the general tendency towards narrowness in training. The study of logic he especially recommends, — “it is to language and grammar what mathematics is to common sense;” “mathematics is the etherealisation of common sense;” “more ships have been lost through bad logic than through bad seamanship.”

In 1839 he went to St. Peter’s College, Cambridge, graduating in 1845. Among the wranglers he was placed second, but his originality and power gained for him the highest mathematical honour, — the Smith’s Prize. At Cambridge, as in Glasgow, he was noted for his wide sympathies and attainments, not in science alone, but in other fields as well. In mental and physical recreations he participated enthusiastically, and he enjoyed to the full the social, athletic, and intellectual life of an old English university. He was President of the University Musical Society, won the Colquhoun Sculls, and rowed in his college boat when second in the Cambridge races. The years spent at his “revered and loved” St. Peter’s College are still affectionately remembered. A few years ago, as a token of gratitude, he presented it with an electric installation; and the Fellowship bestowed on him in his youth, resigned on his marriage, and reconferred in 1872, he values among the highest of the recognitions of his work.

From Cambridge he went to Paris, studied for a time under the famous Regnault, and continued the valuable original contributions to science which he had begun at Cambridge.

His early papers are remarkable and contain germs developed in his later work. His first published paper, written at the age of sixteen and dated Frankfort, July, 1840, Glasgow, April, 1841, appears in the Cambridge Mathematical Journal, May, 1841. It was a defence and elucidation of certain fundamental theorems in Fourier’s “Harmonic Analysis,” the truth of which had been questioned by Kelland. This he followed up in 1842 by a paper “On the Uniform Motion of Heat in Homogenous Solid Bodies, and its Connection with the Mathematical Theory of Electricity.” In it he displayed some of the spirit now recognised as characteristic of his work. Pointing out the analogy between the flow of heat in solid bodies and the theory of electric and magnetic attraction, he made use of known theorems in heat in order to obtain solutions of problems in electricity and magnetism.

His results had, as he afterwards heard, been anticipated by Green, but the beautiful method which he adopted was entirely original, and has proved a fruitful conception in electric and magnetic problems. With some difficulty he was able to unearth a copy of Green’s memoir, and had it published in English in Crelle’s German Mathematical Journal. Charmed by “Fourier’s great mathematical poem,” as in later years he called it, he has never wearied of proclaiming its beauties, and in 1880 he contributed a valuable compendium of the Fourier mathematics to the Encyclopaedia Brittanica.

In 1846 he became attached by an additional link to Glasgow, when appointed professor of natural philosophy in his alma mater, in succesion to Dr. Meikleham. Six years later he married Margaret, daughter of Walter Crum, Esq., F.R.S., of Thornliebank; she died in 1870.

Although only twenty-two years of age at the time of his appointment, William Thomson had already made a reputation. He had published nearly a score of papers, chiefly on the theory of heat and static electricity, bearing the stamp of originality and promise. In reference to his candidature one of his Cambridge tutors wrote: — “He is recognised here by the most competent judges as the first man of LORD KELVIN science of the rising generation in this country.”

The anticipations of his teachers have been amply fulfilled, and the confidence of the University of Glasgow has been repaid by a brilliant, faithful and invaluable service of more than half a century.

His inaugural dissertation, “De Motu Caloris perTerrae Corpus,” dealing with a method of finding absolute geological dates from observations of underground temperatures, was founded on a paper written in 1844, “Notes on some Points in the Theory of Heat.” The further development of this subject appears in many later papers, contributed chiefly to the Royal Society of Edinburgh, and the Geological Society of Glasgow.

At the British Association meeting in 1885 he explained the value, and urged the need, of special geothermic surveys, and these have since been largely carried out. Forbes’ observations on underground temperature in different strata in the Edinburgh neighbourhood gave Thomson the data necessary for estimating approximately the age of the earth. He first showed how the Fourier analysis gives a more accurate and complete reduction of the observations; he then applied it to the results of the five years’ observation by Forbes, supplemented by those of thirteen additional years. In this way he obtained the factors on which he based his calculation — the average diffusivity for heat of surface rock, and the average rate of increase of temperature downwards.

In a paper read to the Royal Society of Edinburgh in 1862, “On the Secular Cooling of the Earth,” he discussed the origin of underground heat; showed that the hypothesis of chemical action and Poisson’s hypothesis as to the previous journey of the earth through a hotter region of space, were both extremely improbable and incapable of explaining the present state of underground temperature, and concluded by treating the earth merely as a mass of incandescent liquid which, in cooling, has consolidated and is still cooling by radiation of its heat. The problem of finding the date of solidification, involving, as it does, a knowledge of the nature and properties of the interior as well as of the surface strata, was naturally one which did not permit of accurate solution with the insufficient data at his disposal, but after indicating the difficulties and allowing very wide limits he made an estimate. Assuming the temperature of melting rocks to be 7000° F., he showed that if the consolidation had taken place 98 million years ago, the average rate of increase of underground temperature in surface strata would be now somewhat nearly what it actually is, viz., 1° F. for every 50 feet descent.

Further, after making sufficient allowance for the uncertainty in the data and conditions, he asserted the great probability that the earth cannot have consolidated less than 20 million, or more than 400 million, years ago. This fascinating mathematical problem, which, from a consideration of the present circumstances, gives the past thermal history of a body, heated and left to cool undisturbed, is now classic and familiar to every student of mathematical physics. Its practical application to the earth gave decisive time limits within which geologists and biologists must confine their evolutionary speculations. Hitherto uniformitarian geologists had indulged their imagination untrammelled by such time limits, and granted similar freedom to biologists. Now Thomson’s 100 million years is generally accepted, — a period formerly regarded as but a second in the geological day. In subsequent papers he adduced additional arguments in support of his views.

Another hypothesis, common among geologists of the period, received its death-blow in a paper delivered in 1862 to the Royal Society of Edinburgh. Thomson showed in this that it was impossible to regard the earth as a molten mass within a solid superficial crust. He found that the effect of gravitation was greater than the effect of elasticity in giving rigidity to the earth’s figure, and the rigidity of the earth, as a whole, must be at least equal to the rigidity of steel, — a prediction afterwards verified by Mr. George Darwin from a consideration of the lunar fortnightly tides. If the interior were liquid, it would be subject to the tide generating influence of the sun and moon. Unless the crust were preter-naturally stiff, it would yield, so that the tides would be imperceptible. The forces to which such a crust would be subject would assuredly break it unless it were infinitely strong. Rocks, being denser when solid than when liquid, the equilibrium of the crust would be unstable if placed over a liquid. But in reality a molten mass would solidify gradually by the cooling of the surface and the falling in of the cooled part towards the centre, the mass finally becoming solid on the whole, with only vesicles containing molten matter.

Other valuable papers, given to the Geological Society of Glasgow, deal with geological time, dynamics and climate, the internal condition of the earth, polar icecaps and similar questions. His contributions to astronomical physics deal with such subjects as the mechanical energies of the solar system, the mechanical value of a cubic mile of sunlight, the origin, total amount and annual loss of sun heat, the sun’s present temperature, its age, future state, present condition, and the sources of its future supply. He accepts Helmholtz’s view that the sun was formed by the mutual attraction and conglomeration of meteorites, which, falling together, produced the heat by transformation of their energy, and that the supply is being continued by the further contraction of the sun and transformation of potential energy to heat.

He shows that the sun’ s original heat and annual supply, though perhaps partly chemical, must be mainly gravitational; that, owing to its high specific heat, it must be liquid, and that its annual loss cannot be made up by any influx of intraplanetary bodies, otherwise planetary perturbations would be manifest; nor any influx of extraplanetary meteorites, for of this we would have undoubted evidence. He introduces additional information into the calculation, and agrees with Helmholtz’s estimate that probably the sun’s initial heat was not more than 20 million times the present annual output. In Thomson’s view the sources of solar energy are gradually becoming exhausted, but we may take comfort from his estimate that there still remains of the capital five or six million times the annual draft.

His opinions on terrestrial and astronomical physics were so opposed to the geological and biological thought of the time that, in 1869, he was led into the memorable controversy with Professor Huxley, the most redoubtable debater among natural historians of his day. Views so contrary to existing hypothesis could not well be received without question, but they were gradually entertained and are now generally accepted. Huxley, referring to this spirited controversy when introducing Thomson as his successor to the presidential chair of the British Association in 1871, said of him, “Gentler knight never broke lance.” It was in telegraphy, however, that Thomson first gave evidence of that remarkable combination of mathematical ability and mechanical ingenuity which distinguishes his work. Land telegraphs had already been in use for nine years when the first short submarine telegraph cable was laid, in 1846, in Portsmouth Harbour. Its success created great excitement in scientific and commercial circles. Longer cables were successfully laid, — Dover and Calais in 1850, Holyhead and Howth in 1852, Harwich and The Hague in 1853; and before 1855 there was a network in the Mediterranean, and a cable to the Crimea, which, during its short life of a year, proved invaluable to the British War Office.

The efficiency and economy depended greatly on the “velocity of propagation” of the signals. Currents sent took some time to make their presence felt at the other end of the cable, and intermittent currents were seriously enfeebled during transmission. The difficulty demanded and received the attention of electricians. It was found from experiments on the Harwich cable that the explanation must be sought in the electrical capacity of the cable, and it seems only natural that the clue should be discovered by Faraday, whose researches on electrical capacity have obtained appropriate recognition in the association of his name with the unit in which that quantity is now measured. Faraday recognised that the wire of the cable, and the insulating covering, and the water outside form a condenser.

Thomson took the subject up. He found, first, a mathematical expression for the capacity, and showed how it depended on the dimensions and the insulating material used. Further, in 1854, first in a letter to Stokes, and afterwards, in the following year, in a communication to the Royal Society, he gave the investigation of the problem, leaving out of account the effect of electromagnetic induction, which he showed to be comparatively small in a long cable. The “ law of squares “ was the result. An electric impulse applied to one end of a cable is not transmitted instantaneously to the other end, but gradually increases, attains a maximum, and finally falls to zero. In cables similar in material and section, but of different lengths, the time taken to experience the maximum effect, or any stated proportion of the maximum effect, at the receiving end, is proportional to the square of the length of the cable; in cables of the same length, but of different sections, it is proportional to the resistance and the capacity.

The effect of the various properties is well illustrated by the hydraulic analogy which he gave. Imagine a tube filled with a fluid transmitting an impulse from one end to the other. If the tube were rigid, and the fluid incompressible and without inertia and viscosity, the impulse would be transmitted from one end to the other instantaneously and without diminution. Make the tube elastic, or the fluid compressible, and you have the “capacity” effect; endow the fluid with inertia, and you have the “self-inductive” effect; give it viscosity, and you have the effect of the “resistance” of the cable. In long cables the inertia effect, proportional, as it is, to the length, is small compared to the capacity effect which is proportional to the square of the length.

While Thomson was busy with the theory of telegraph cables, pointing out the difficulties to be encountered in the laying and commercial working of long cables, urging the necessity for new methods of transmitting and receiving signals, explaining the scientific design of cables, and showing how to attain the most economical construction, Whitehouse, electrician to the Atlantic Telegraph Company, and others, were busy experimenting with existing cables and experimental lines, and Cyrus Field and Gisborne were discussing the financial side of the question. Mathematicians, engineers and financiers were all bending their energies towards the task of spanning the Atlantic. Whitehouse, from a valuable series of experiments, showed that the signal took 1 1/2 seconds for transmission through his experimental cable, 1125 miles long, and, according to the “law of squares” under similar conditions, 6 seconds would be required for the transmission of a signal from Ireland to Newfoundland, which was about twice that distance. On the whole, his results seemingly contradicted the theory, which he accordingly stoutly denied; but Thomson explained the apparent difficulties and discrepancies, and showed that, far from contradicting theory, Whitehouse’s results really confirmed it.

The practical difficulties to be overcome were no sooner recognised by Thomson than he at once set himself to surmount them. Capacity and resistance were two inherent evils, but their effects could be lessened by scientific design and the use of the most suitable material. He investigated the conductivity of copper supplied by different makers as “pure,” and found it to vary by as much as 50 per cent. Even specimens from the same cable gave widely different results. Further, he found that the differences were due to differences in the process of manufacture and to small amounts of impurities in the copper.

This discovery had a very important bearing on the cost and efficiency of a cable, and he succeeded in getting the directors of the Atlantic Telegraph Company to specify for the first time, and the contractors to supply, “high conductivity” copper for the extra length of cable required to replace the part lost in the two unsuccessful attempts of 1857. It was very evident that the instruments required must far surpass in delicacy existing “land” instruments, even when backed up with enormous battery power. He, therefore, turned his attention to improvements in the testing and working of electric telegraphs. His first master patent of 1858 includes keys for transmitting and the mirror galvanometer for receiving the messages. The most sensitive receiver previously used was a galvanometer constructed on Weber’s principle, — a magnetised steel disc with a polished surface suspended by a long silk fibre in the centre of a coil of wire, the deflections being read by means of a telescope and scale.

The well-known Thomson mirror galvanometer surpassed its immediate predecessor even more than the modern bicycle excels the old velocipede or boneshaker. The heavy steel disc was replaced by one or more small magnets of fine flat steel, fixed to the back of a tiny circular mirror of plain or concave silvered glass. The whole system weighed only about half a grain, and was easily suspended by a single silk fibre, which could be made very short without manifesting any appreciable torsion effects. The mirror and magnets were suspended inside a horizontal brass tube only slightly larger in diameter; glass plates were screwed so close behind and in front of the mirror as to enclose it, with just sufficient clearance, in a small chamber; thus “ air damping “ was introduced, which brought its motions quickly to rest.

The tube was placed inside a coil which surrounded it closely, and any deflection of the mirror, produced by a current passing round the coil, was detected by means of a beam of light falling from a lamp on to the mirror and thence deflected on to a scale. For use on board ship the mirror, to prevent swinging, was suspended, top and bottom, by a stretched silk fibre, while to get rid of the disturbing influence of the ship’s magnetism or moving masses of iron, the instrument was screened by a soft iron case. Its wonderful sensitiveness, accuracy and stability permitted it to be used on board ship for even the most delicate tests. It has been proved capable of detecting a signal sent across the Atlantic by a miniature battery consisting of a thimble, a needle and some salt water.

The year 1858 saw the Atlantic Telegraph Company prepared to renew their efforts, better equipped and possessed of the experience gained from the two failures of the previous year. At the request of his brother directors, Thomson took upon himself the duties of electrician on board H. M. S. Agamemnon, which had been placed at the disposal of the company. The Niagara was lent by the United States government, and these two ships successfully established communication between Ireland and Newfoundland.

On August 6 Thomson’s instruments delivered the first message and proved the commercial feasibility of an Atlantic cable. When other instruments failed to speak, the mirror galvanometer gave 2 1/2, words per minute, even with defective transmitting arrangements. Unfortunately the cable, hurriedly constructed, seriously impaired during enforced delay, and damaged by the strains of coiling and uncoiling, gradually gave way and failed, but in its short life of a fortnight it succeeded in delivering 400 messages. The electricians and engineers, having tasted the sweets of success, were rendered more confident, the promoters still remained sanguine, but the shareholders declined to risk more money on the scheme; and in an enterprise of this magnitude complete success can be obtained only when sufficient capital supports sufficient science.

The last word spoken, — “Forward,” — was a word of good omen. For a time the scheme lay dormant, but the engineers were busy. Thomson continued his mathematical and experimental investigations and still further improved the instruments. In 1865 another attempt was made to lay a new cable, constructed on improved and scientific principles, but an unfortunate accident led to its breakage. Success, however, finally attended the labours which had been pursued with unshaken faith and dauntless energy.

On July 15, 1866, the Great Eastern permanently established the communication for which they had so long striven, and the triumph was crowned by the recovery and completion of the cable lost in 1865. We may well apply to this great achievement the words Thomson spoke from the presidential chair of the Royal Society in 1893:

“Tribulation, not undisturbed progress, gives life and soul, and leads to success where success can be reached in the struggle for natural knowledge.”

Professor Thomson’s great share in the final triumph was suitably recognised when, on the return of the expedition, he received, with several of the other heroes, the honour of knighthood. Some remarks he made at a banquet given in their honour by the Lord Mayor of London are worthy of quotation as illustrating what has been a guiding principle in his work: —

“Unless men of science pursue their studies out of a pure love of knowledge or from an abstract desire to become acquainted with the laws of nature, they will seldom carry on their labours with success; but, at the same time, no greater reward could crown their investigations than when, as in the case of electric telegraphy, they are the means of conferring a practical service on mankind, the value and importance of which are admitted on all hands. …My only object in these remarks is to point out that science, to be true to itself, must be followed for its own sake, and that all the most important services it has rendered to mankind have been the result of arduous investigations, carried on by men animated with the hope of no other reward than that which awaits every sincere and industrious student of nature.”

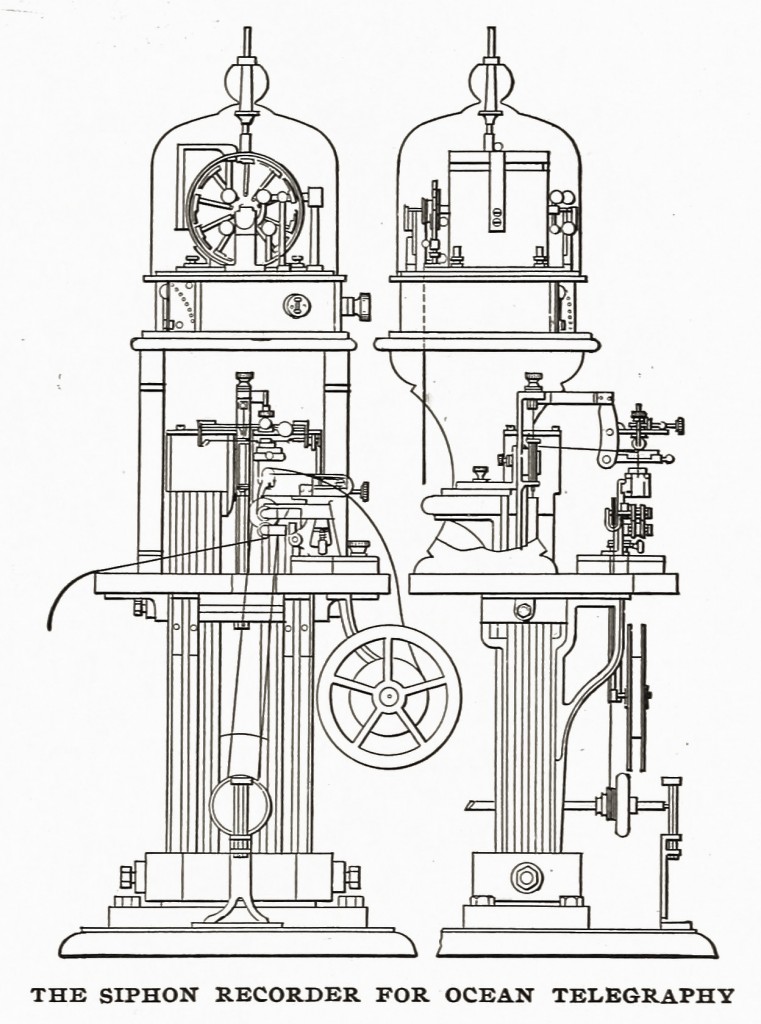
The growing prosperity of the cable demanded improvements in the instruments. In conjunction with Varley and Fleeming Jenkin, various sending instruments were patented, and in 1867 Thomson invented his graphic receiver, the siphon recorder, which, since 1870, has been employed on all cables except those very few on which the mirror galvanometer still survives. In this marvellously delicate instrument the relation between the coil and magnet of an ordinary galvanometer is reversed, and a new principle is thus introduced which has since been utilised in the, class of galvanometers known as D’Arsonval’s.

The current which passes through the cable is led into a rectangular coil suspended between the poles ‘of a powerful magnet. An electromagnet was used at first, but this has been superseded by a permanent magnet. The motions of the coil are communicated to a very fine capillary glass siphon, of which the shorter leg dips into the ink reservoir, while the longer acts as a pen.

The paper is a tape, carried by clockwork over a brass table close to the pen, but avoiding contact and friction with it. The ink is electrified by means of a small clockwork- driven induction machine, or the siphon is caused to vibrate rapidly by mechanism, and very minute drops of ink are shot on to the passing paper. As in the mirror galvanometer, the Morse code of signals is used, excursions of the coil to one side or other corresponding to dots or dashes, and the message thus appears on the tape as a wavy line which is easily read. The speed of signalling depends on the length and construction of the cable and the expertness of the operator. On a short line as many as 135 words per minute can be received, but on a long cable 20 to 30 are the average.

After 1866 Thomson was adviser to a number of other cable companies, and his annual six months’ freedom from professional duties permitted him to take part in many more expeditions. On one of these, detained a fortnight in Funchal Bay on the way to South America, in 1873, he met Frances Anna, daughter of C. R. Blandy, Esq., of Madeira, whom he married in 1874.

Nothing better exemplifies the intense interest Thomson took in everything than his connection with the science of navigation. An early association with nautical matters was revealed in a speech delivered by him at the unveiling at Glasgow University of a memorial bust to a companion.

“My earliest recollections of Lord Sandford,” he said, “are not of his brilliant career as a student in the universities of Glasgow and Oxford, but as a boy of my own age, playing on the college green, making ships and sailing hem in the Molendinar Burn, now flowing under the ground, not like a modern terrestrial river at all, but rather like another river known in the classics. Black as Styx now, it was black enough then when Frank Sandford and I used to make docks on its banks, to moor our ships and bring them into the harbour, and when we used to fall into the muddy stream itself. These were bright and happy days in the old college and the old college green of Glasgow, full of memories to myself, too touching for me to speak of now; they are among the most treasured and valued possessions of my memory.”

His telegraphic experiences seem to have whetted his appetite for the sea. For nearly 20 years from 1870 he spent most of his vacations on his yacht, the Lalla Rookh, a schooner of 126 tons, sometimes cable testing, sometimes on pleasure cruises. Lady Kelvin also is an enthusiastic sailor, and their honeymoon was spent on board, in a twelvedays voyage from Madeira to Cowes.

It is little wonder that the science and practice of navigation soon benefited by his fondness for the sea. In 1872 he introduced a great improvement in the apparatus required for taking deep-sea soundings. He showed the great advantages to be derived by using, instead of hemp rope, steel pianoforte wire, which combined small size, lightness and strength, weighing only about 1 1/2 pounds per 100 fathoms, and having a tensile strength of 240 pounds. In deep-sea soundings of from 2000 to 3000 fathoms, the operation could be performed by three or four men instead of a ship’s crew or a donkey engine; a weight of 34 pounds was sufficient for a sinker, and was brought back with the wire recovered, instead of a weight of two or three hundred pounds, left at the bottom; and for navigational purposes it permitted, what had not been previously even dreamed of, — flying soundings in 100 fathoms from a ship running at 16 knots. The method and apparatus devised were originally used in the laying of the Brazilian cable and proved most valuable.

The depth recorder is a useful addition. It consists of a cylinder into which a piston is gradually pushed by the water pressure against the action of a spiral spring. The final position of the piston, and, hence, the depth, is shown by a small index which is carried along a scale. Sometimes it is found convenient to use a chemical recorder. A long, fine glass tube, closed at one end, is coated inside with orange-colored chromate of silver, and the depth is ascertained from the compression of the air, indicated by the chromate turning white throughout the portion of the tube into which the sea water has forced its way.

The mariner’s compass next claimed his attention. In 1874 the first part of an article on “The Mariner’s Compass” appeared in Good Words, — “To be continued,” — but not until 1879 was the second part printed. In writing it and considering the dynamics of the problem, Thomson saw how vastly the compass might be improved, and could not bring himself to describe the then existing compass when he saw how great a change was necessary, and felt that it would soon be superseded. The new compass was patented in 1876. As its design was completely at variance with prevalent practice, it is scarcely to be wondered that navigators, — proverbially conservative in everything relating to their art, — refused a welcome to an innovation based on scientific reasoning which failed to find favour in the eyes of the Astronomer Royal of the day.

Slowly and surely, however, its merits became recognised. In 1889 Sir William Thomson’s 10-inch standard compass was finally adopted by the British Admiralty, and now no ship of worth is without one or more of the numerous patterns of his compass. Since 1840 the Admiralty compass had a card 7 1/2 inches in diameter, but cards up to 15 inches were used in merchant ships, as they were found to be steadier at sea. It had generally been considered that the magnet, or magnets, ought to be of great magnetic moment so that the directive influence of the earth’s magnetism might be greater; but if the moment was great, the period of vibration of the card was small, and unsteadiness was the result. The period was lengthened by adding weights in some manner, and thus steadiness was gained at the expense of friction at the point on which the card was supported. More drastic measures were occasionally employed to make it less lively, and the methods practised included filling the cup with dust and blunting the point! Thomson showed, however, that short magnets of small magnetic moment were desirable, not only because they allowed the possibility of a long vibration period with a light card and consequent diminution of friction, but also because they permitted the use of steel magnets and soft iron masses so disposed as to correct completely all the various errors due to the magnetic influence of the ship. This last quality was rendered all the more desirable owing to the more extensive use of iron in shipbuilding.

The problem then was, to construct a card sufficiently rigid, large, and light, with magnets short and of small moment, yet strong enough to give a controlling force sufficient to make the friction inappreciable; and the solution is a wonderful example of delicate engineering. In the centre is a little inverted sapphire cup borne on a supporting iridium point and carrying a small aluminium disc. This disc forms the hub to which the light aluminium rim, 10 inches in diameter, is connected by spokes of silk threads. The card is reduced to a ring of thin paper fixed to the rim and the threads, and the evil effects of warping are very simply avoided by slitting the paper-ring at intervals. The magnet system of eight small needles, from 2 1/2 to 3 1/2 inches long, is constructed like a rope ladder and slung by silk fibres to the spokes. Compared with the old card, the weight is about one-seventeenth, — 170 grains instead of 6 ounces; the magnetic moment is one-thirteenth, and the period of vibration is twice as great, being 42 seconds. The card is only one of the improvements, and subsequent patents deal with various accessories and methods for adjustment and correction.

Sumner’s method for finding the position of a ship at sea found in Thomson a very warm advocate. Its utility was obvious, but it was not widely known, and the calculations to be performed, simple though they were, had still further to be shortened before there was any hope of the method becoming generally used. In 1876 he published a complete set of tables by means of which the arithmetical operations were so much shortened that they required neither more time nor skill than the methods commonly practised. So greatly has Kelvin contributed to the safety of navigation that he is regarded by appreciative mariners as an incarnation of the “cherub that watches over poor Jack.”

IN his dual capacity as a scientist and a sailor, Thomson recognised the deficiency of trustworthy and adequate knowledge of the tides and launched forth on a grand scheme for investigating and predicting the tides at all the ports in the world. The theory of the tides was known. It had been well worked out by Laplace, Airy and others, who showed chat the height of the tide at any time and at any place could be found by adding together the effects at that time of a certain number of constituent tides, each a simple harmonic function of the time. In other words, the tide-time curve was the sum of a certain number of constituent sine curves. The scheme involved the finding, from years of observation at the different ports, of the total tide-curve for each port, and the determination from it of the constituent tide-curves. The twenty chief constituents, requiring forty constants to specify them, may be determined from observations extending over one year.

In 1867 he brought the subject before the British Association, with the result that a committee, which afterwards rendered valuable service, was formed “for the purpose of promoting the extension, improvement, and harmonic analysis of tidal observations.” The ingenious instruments devised by him, and extensively used to facilitate the recording and perform the calculations mechanically, are fully described in the Proceedings of the Institution of Civil Engineers for 1881, in his paper on “The Tide Gauge, Tidal Harmonic Analyser, and Tide Predicter.”

Perhaps no science owes more to Lord Kelvin’s genius than that of thermodynamics. We may regard the years from 1840 to 1850 as the dawn of the modern dynamical theory of heat, — that transition period which witnessed the death of the old idea, heat, — “a substance, invariable in quantity, not convertible into any other element, and incapable of being generated by any physical agency,” and the birth of the new and all-pervading idea, heat — “a mode of motion.”

In 1820 Carnot had given forth his “Theory of the Motive Power of Heat,” but he was in advance of the age and little attention was paid to it until about a quarter of a century afterwards. The experiments of Rumford and Davy had thrown discredit on the existing ideas regarding the nature of heat, and Carnot fully appreciated the difficulties and possibilities raised by them; but, nevertheless, for want of a better, he accepted the “material” theory.

Carnot’s ideal engine, in which any working substance could be used, produced power in the transference, by a certain steady cycle of operations, of heat from a hot body, (the source), to a cold body, (the condenser). It required, as its fundamental axiom, the assumption that the heat taken in at the source is equal in quantity to that given out by the condenser. Motive power was considered to be derived from heat in much the same way as from water flowing from a higher to a lower level; heat at a high temperature possessing greater capacity for mechanical effect; and though for years engineers had used condensing engines, strange as it may now seem, they tacitly admitted that, in Carnot* s engine, the heat which left the boiler entered the condenser undiminished. In a paper to the Philosophical Magazine, in 1848, Thomson proposed an absolute thermometric scale, founded on Carnot’ s theory, and independent of the properties of any particular substance. He modified it in 1854 so as to make it more convenient in practice. The scale has proved extremely useful in thermodynamic investigations, and possesses the additional advantage that it agrees with the practical standards, — air thermometers, — as closely as they do among themselves. The paper gave abundant evidence of the state of doubt then prevailing. He referred to some of Joule’s experiments, and appealed for further and fuller experimental investigations on the nature of heat.

In the same year, in a paper on “The Theory of Electro-magnetic Induction,” he gave a simple proof of Neumann’s theorem on the intensity of the current induced in a closed conductor by the relative motion of a magnet. He based it on the axiom that the amount of work expended in producing the relative motion on which the electro-magnetic induction depends must be equivalent to the mechanical effect lost by the current induced in the wire; and snowed, first, that “the amount of mechanical effect continually lost or spent in some physical agency (according to Joule, the generation of heat) during the existence of a galvanic current in a given closed wire is, for a given time, proportional to the square of the intensity of the current.”

In the following year he gave a full account of Carnot’ s theory to the Royal Society of Edinburgh, and obtained, from examination of results of Regnault and other observers, a striking confirmation of the theory so far as regards different working substances. At the same meeting his brother, Professor James Thomson, gave a modified specification of Carnot’ s cycle which obviated the necessity of considering heat as material, and also showed how, according to the theory, the freezing point of water ought to be lowered, by application of pressure, 0°.0075 C. for each additional atmosphere. This striking prediction was experimentally verified by Professor William Thomson in the following year. Again Thomson pointed out the difficulties in the way of the theory, and emphasised the necessity of experiments which would supply either explanations or an entirely new basis for the theory of heat. The paper contained also an instructive table of the efficiency and economy of the best engines and boilers of that date, comparing the actual and theoretical duties; and it is interesting to note that he suggested, as a means of obtaining a closer approach to the theoretical duty, the use of what is now known as superheated steam.

Meanwhile, Mayer, in Germany, had been experimenting on the relations existing between heat and work, and Joule was patiently and incessantly adding experiment s after experiment to his grand series on the mutual relations of electric, magnetic, and chemical actions, and work and heat, forging link after link in the chain which now binds them together in one connected whole. One of Joule’s results, — unfortunately the only one with which his name is popularly associated, — was the discovery of the numerical relation between work done and heat* produced. His results seemed to be entirely at variance with Carnot’ s theory, which he accordingly denied, though it was confirmed in many remarkable ways by experiment. One of the obstacles in the way of accepting Joule’s ideas lay in the absence of special experiment to show the direct conversion of heat to work with the same numerical result. It seemed to stand, Joule vs. Carnot.

The position of matters at the time is well shown in the following extract from a speech delivered by Lord Kelvin when he unveiled the Joule statue’.in Manchester Town Hall on December 17, 1893:—

“I can never forget the British Association at Oxford in 1847, when, in one of the sections, I heard a paper read by a very unassuming young man who betrayed no consciousness in his manner that he had a great idea to unfold. I was tremendously struck with the paper. I, at first, thought that it could not be true, because it was different from Carnot’s theory, and immediately after the reading of the paper I had a few words of conversation with the author, James Joule, which was the beginning of our forty years’ acquaintance and friendship.”

“On the evening of the same day that very valuable institution of the British Association, — its conversazione, — gave us opportunity for a good hour’s talk and discussion over all that either of us knew of thermodynamics. I gained ideas which had never entered my mind before, and I thought I, too, had suggested something worthy of Joule’s consideration when I told him of Carnot’s theory. Then and there, in the Radcliffe Library, Oxford, we parted, both of us, I am sure, feeling that we had much more to say to each other and much matter for reflection in what we had talked over that evening.”

“But what was my surprise a fortnight later when, walking down the valley of Chamounix, I saw in the distance a young man walking up the road towards me and carrying in his hand something which looked like a stick, but which he was using neither as an Alpenstock nor as a walking stick. It was Joule with a long thermometer in his hand, which he would not trust by itself in the char-a-banc coming slowly up the hill behind him, lest it should be broken. But there, comfortably and safely seated on the char-a-banc, was his bride, — the sympathetic companion and sharer in his work of after years. He had not told me in Section A or in the Radcliffe Library that he was going to be married in three days; but now, in the valley of Chamounix, he introduced me to his young wife. We appointed to meet again a fortnight later, at Martigny, to make experiments on the heat of a waterfall (Sallanches) with that thermometer, and afterwards we met again and again and again, and from that time, indeed, remained close friends till the end of Joule’s life.”

It is noteworthy that the chief workers in the new field, Joule, Thomson, Helmholtz, Rankine, and Clausius, were all young men under thirty, Thomson being the youngest. The materials were hot, the man was ready, and in 1851 Thomson struck the blow that welded heat and dynamics together, and created the new science of thermodynamics. His paper to the Royal Society of Edinburgh, “On the Dynamical Theory of Heat,” reconciled Joule and Carnot, scattered all doubts, placed the whole subject on a satisfactory and scientific basis, and gave a wonderfully complete mathematical treatment. The relations between heat and electricity were at once subjected to scrutiny in the new light and also received mathematical consideration.

One of the first fruits was Thomson’s prediction that an electric current, in passing through an unequally heated conductor, must produce different thermal effects according as it passed from hot to cold or from cold to hot in the same metal. This phenomenon, — the “Thomson effect,” — predicted from theoretical considerations, was experimentally shown by him to exist three years later in one of an extensive series of investigations on the thermo-electric properties of different metals, and the alteration produced by mechanical and magnetic strains. The thermo-electric diagram which exhibits so clearly all the effects and their relations was first suggested by Thomson.

Other interesting conclusions were made as a result of the new thermodynamic theory. For example, from his value of Carnot’s function, calculated from Regnault’s experiments, he showed that the existing determinations of the specific heat of air at constant pressure were from 10 to 20 percent, too high, and gave as its value 0.2374, which is almost exactly the value found experimentally by Regnault in the following year.

In 1852 he undertook, with Joule, a series of experiments on the thermal effects of fluids in motion, which extended over a period of about ten years and yielded many valuable results. They showed the very approximate truth of Mayer’s hypothesis that the heat evolved from air, compressed and kept at a constant temperature, is mechanically equivalent to the work done upon it, and enabled a comparison of the scales of the air and absolute thermometers to be effected. Taken together with Regnault’s results on the latent heat and pressure of saturated steam, they gave increased strength to the suspicion entertained by Thomson, Rankine and others that the density of steam deviated very considerably from what was given by the ordinary gaseous laws.

Thomson’s paper on “The Dynamical Theory of Heat” and its exposition of the grand principle of the conservation of energy, for which Joule furnished the experimental foundation, was followed immediately by other papers on kindred subjects. In the same year, 1851, in his paper “On the Mechanical Theory of Electrolysis,” he showed how to determine the electromotive force of a primary battery, — a Daniell cell, — from the chemical actions going on within it, and gave also for the first time the true law for the efficiency of an electromotor. During the next two years, — a period of remarkable activity, — he gave a number of papers on such subjects as on the sources of heat generated by the galvanic battery; on the mechanical action of radiant heat or light; on the power of animated creatures over matter; on the sources available to man for the production of mechanical effect; on the mechanical values of distributions of electricity, magnetism and galvanism; and on the restoration of mechanical energy from an unequally heated space.

In 1852 he enunciated the doctrine of “The Dissipation of Energy.” It was the outcome of the consideration of the reversibility of processes for the transformation of energy, and was founded on the axiom on which he based his proof that no engine could be more efficient than a perfectly reversible one: —

“It is impossible by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects. If this axiom be denied for all temperatures, it would have to be admitted that a self-acting machine might be set to work and produce mechanical effect by cooling the sea or earth, with no limit but the total loss of heat from the earth and sea, or, in reality, from the whole material world.”

The following extracts are interesting: — “The considerations of ideal reversibility by which Carnot was led to his theory, and the true reversibility of every motion in pure dynamics have no place in the world of life. Even to think of it (and on the merely dynamical hypothesis of life we can think of it as understandingly as of the origination of life and evolution of living beings without creative power), we must imagine men with conscious knowledge of the future, but no memory of the past, growing backward, and again becoming unborn; and plants growing downward into the seeds from which they sprang. But the real phenomena of life infinitely transcend human science, and speculation regarding consequences of their imagined reversal is utterly unprofitable. Far otherwise, however, it is in respect of the reversals of the motions of matter, uninfluenced by life, a very elementary consideration of which leads to the full explanation of the theory of the dissipation of energy…”

“Exhaustive consideration of all that is known of the natural history of the properties of matter, and of all conceivable methods for obtaining mechanical work from natural sources of energy, whether by heat engines, or electric engines, or water-wheels, or windmills, or tidemills, or any other conceivable kind of engine, proves to us that the most perfectly designed engine can be only an approach to the perfect engine, and that the irreversibility of actions connected with its working is only part of a physical law of irreversibility according to which there is a universal tendency in nature to the dissipation of mechanical energy: and any partial restoration of energy is impossible in inanimate material processes, and is probably never effected by means of organised matter, either endowed with vegetable life, or subject to the will of an animal.”

A popular statement of the doctrine is contained in the following quotation: — “Daring any transformation of energy of one form into energy of another form there is always a certain amount of energy rendered unavailable for further useful application. Xo known process in nature is exactly reversible. — that is to say. there is no known process by which we can convert a given amount of energy of one form into energy of another form, and then, reversing the process, reconvert the energy of the second form thus obtained into the original quantity of energy of the first form.”

“In fact, during any transformation of energy from one form into another, there is always a certain portion of the energy changed into heat in the process of conversion, and the heat thus produced becomes dissipated and diffused by radiation and conduction. Consequently, there is a tendency in nature for all the energy in the universe, of whatever kind it may be. gradually to assume the form of heat. and. having done so, to become equally diffused. Now, were all the energy of the universe converted into uniformly disused heat, it would cease to be available for producing mechanical effect, since for that purpose we must have a hot source and a cooler condenser. This gradual degradation of energy is perpetuallv going on, and. sooner or later, unless there be some restorative power of which we. at present, have no knowledge whatever, the present state of things must come to an end.”

In 1852, also, in a paper on “The Economy of the Heating or Cooling of Buildings by means of Currents of Air,” he proposed and investigated methods by means of which cooling and heating could be performed with the consumption of a much smaller quantity of coal than was required by direct means. For heating purposes, air from the atmosphere was expanded in a cylinder and sent to a receiver, its temperature being maintained constant by heat drawn from the surroundings. It was then heated by compression in a second cylinder and discharged. For cooling, the reverse cycle was to be used: air was compressed in one cylinder and discharged to the receiver, the surroundings keeping the temperature constant. It was then cooled by expansion in, and discharged from, the second cylinder. The method of heating remains yet unrealised; but the method of cooling has been realised in several refrigerators.

Thomson’s papers on “Transient Electric Currents,” which were given in 1853 to the Glasgow’s Philosophical Society and to the Philosophical Magazine, contain a number of interesting results and suggestions. Here he suggests a method of measuring electrostatic potentials by weighing, which he afterwards adopted in various instruments. Here also, proceeding from the equation of energy, he investigated the discharge of a condenser through a resistance possessed of self-induction, and showed that, under certain circumstances, the discharge would be oscillatory in character. He suggested that this might be an explanation of the multiple flashes of lightning which sometimes occur.

Helmholtz had previously come to suspect surgings to exist from consideration of the experiments of Reiss and of Wollaston on the magnetic and electrolytic effects of the discharge. Thomson’s paper also suggests a method of investigating the discharge by means : I a revolving mirror, which Feddersen, in 1861, successfully adopted. The phenomenon of oscillatory discharge is rendered all the more interesting because it formed the starting-point from which Hertz commenced his later brilliant researches on electric waves.

Notwithstanding his labours and successes in other fields, which alone would place him in the first rank of the men of science of the century, perhaps it is with the theory and the practical applications of electricity and magnetism that Lord Kelvin will be forever most prominently, as he is most popularly, associated. Most of his earlier electrical papers were on electrostatics, and in 1845, when twenty-one years old, he contributed two papers to the Liouville Mathematical Journal. In one of these he discussed Sir William Snow Harris’s experiments, to which the Copley Gold Medal of the Royal Society had been awarded.

These were apparently at variance with Coulomb’s laws, but Thomson showed that they really confirmed them when proper account was taken of the circumstances under which the experiments were performed. In this paper we see also the first attempt to found the mathematical theory of electricity on Faraday’s discovery of induction. The second paper showed how it was possible to solve problems on the distribution of electricity on conductors by the use of what he called “electrical images,” which gave extremely simple and elegant solutions to difficult problems. Two years later he gave another paper on the same subject to the British Association.

At this time progress in electric investigation was greatly hampered and comparison of results rendered difficult and tiresome by the various arbitrary electric units adopted by different experimenters. Gauss had already propounded the absolute system of dynamical and magnetic units which have proved of such immense value, and in 1851 Weber extended it to electromagnetism. Thomson immediately welcomed and adopted Weber’s units, and in the same year prepared a paper on “Applications of the Principle of Mechanical Effect to the Measurement of Electromotive Forces, and of Galvanic Resistances in Absolute Units.”

Weber’s unit of electromotive force was derived from the idea of cutting lines of force. Thomson introduced the idea of mechanical effect, and showed that “if a current of uniform strength be sustained in a linear conductor, and if an electromotive force act in this conductor in the same direction as the current, it will produce work at a rate equal to the number measuring the force multiplied by the number measuring the strength of the current.” Here also, for the first time, the electromotive force of a Daniell cell is calculated in absolute units, and we find the novel method of measuring the absolute resistance of wire by finding the heat produced in it by a known current passing through it, —the beginning of absolute electric measurements.

Thomson warmly advocated the adoption of the absolute system, both for purposes of investigation and for telegraphic work, which was then the only important practical application of electricity; and in 1861 he obtained the appointment of a committee of the British Association on electrical standards. In this committee he was a prominent and indefatigable member, and to its labours during ten years must be ascribed much of the rapidity of the progress in electric lighting and transmission of power, the pioneers of which found themselves, when their time came, possessed of a perfect system of absolute units and realised practical standards, which suited their needs, and simplified the required formulae and calculations.

The adoption of the units was one desirable end to be gained, but instruments to make accurate] measurements simply and conveniently had yet to be devised. Lord Kelvin’s feelings on the subject of measurement generally are well seen in the following quotation: —

“I often say that when you can measure what you are speaking about and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely, in your thoughts, advanced to the stage of science, whatever the matter may be.”

In 1853 he showed how to construct an instrument to measure electrostatic potential in absolute units; and two years later he carried it into practice, exhibiting his “absolute electrometer” to the British Association. With this instrument absolute electrostatic measurements were made for the first time in 1860 during his researches on the electromotive force required to produce a spark in air. Briefly, the essential part of it consists of two insulated circular brass plates; one is capable of being moved nearer or further away by an ascertainable amount; the other is fixed, and has a circular hole in the centre into which fits, just avoiding contact, a small aluminium disc, suspended by miniature coach springs, and in electrical communication with it.

When the instrument is used heterostatically, an independent source of electrification is required, and this is furnished by a small induction machine, — the well-known Thomson “replenishes.” A small, independent, attracted disc gauge, similar in principle to the main gauge, is used to show if the electrification remains constant during an experiment. The fixed plate and the disc are connected to the replenisher and the movable plate, earthed and brought into such a position that the force of attraction between it and the disc brings the disc to its normal position against the action of its supporting springs, which exert on it a measurable force. The moving plate is then connected to the body or source whose potential it is desired to measure, and its distance is altered till it again brings the disc to its normal position. The distance through which the plate is moved, the force due to the springs, and the area of the disc require to be known to calculate the potential in absolute units.

The same principle of measuring the force of attraction on a disc is used in his long-range electrometer for measuring potentials from 4,000 to 80,000 volts, and in his portable electrometer, which was designed to be as small and compact as possible and convenient to be carried about from place to place for rapid observations of atmospheric electricity. He used another electrometer, with the same general features, in his experiments to find the number of electrostatic units in an electro-magnetic unit of quantity, which was proved to be, as Maxwell’s electro – magnetic theory required that it should be, equal to the velocity of light in air within the limits of accuracy of observation.

In the Transactions of the Pontifical Academy of Rome for 1857, there appears a description of Lord Kelvin’s first divided ring electrometer, which afterwards developed into the well-known Thomson quadrant electrometer, — an instrument invaluable in scientific research and indispensable in every decently equipped laboratory. It is impossible here to give even the briefest description of these well-known instruments; they are described in most text-books.

In 1867 Sir William Thomson reported to the British Association that he had constructed a series of electrometers capable of measuring potentials from 1/400 to 100,000 Daniell cells, these measurements being reducible to absolute measurements by comparison with one instrument of the series. The importance of this enormous stride in the practice of electrical measurement is well seen from the statement in the committee’s report that they “surpass every expectation of practical electricians and furnish a new engine for electrical research.”

The unit of resistance was the first to receive attention, and in 1863-’64 experiments were conducted by Clerk Maxwell and Fleeming Jenkin to determine, by a method proposed by Thomson, the value of the absolute standard and to form from that a material standard of resistance. A year later the committee distributed thirty – three copies of the provisional B. A. unit to be used as standards till a closer approximation to the true ohm should be made. The B. A. unit is still to be met with in resistance boxes; but it was displaced, first by the legal ohm of the Paris Congress in 1882, and afterwards in Great Britain by the Board of Trade ohm, proposed in 1891 and finally adopted in 1894.

Cable telegraphy, undoubtedly, gave the starting impulse to scientific electric measurement. In 1858 it had been put into practice in ascertaining the copper and insulation resistance and the capacity of cables; but it was not till the close of the British Association committee’s work, in 1869, that it became common in Great Britain and America, and not till after the Paris Congress was it usual on the Continent.

It was natural that Lord Kelvin should take a leading part in the rise and development of electric lighting and transmission of power, as well in the generation of electricity as in its measurement. Besides other primary batteries he has given a standard Daniell cell and a tray Daniell for large currents. Various forms of open coil dynamos were proposed by him, and in 1881 he patented a wave-wound disc armature, without iron core.

Ferranti independently invented a somewhat similar machine shortly afterwards, and together they introduced the Thomson-Ferranti alternator, which immediately created a great sensation, as it produced results far in advance of any previously attained, giving about five times the usual output per ton weight. He made numerous contributions to the theory of dynamos and the windings of armatures and field magnets, and drew attention to, and gave a formula for, the pressure produced on the bearings by the gyrostatic action of the armature when the shaft changes its direction, as in a car turning a curve or in a ship rolling.

The transmission and distribution of electrical energy also attracted his attention. In 1879, when giving evidence on electric transmission before a Parliamentary committee, he showed that it was possible to transmit with economy 21,000 H. P. under a pressure of 80,000 volts to a distance of 300 miles. Two years later he gave a paper to the British Association on “The Economy of Metal Conductors of Electricity,” which contained his w r ell-known economic law, applicable, with the necessary changes, to many other questions of economy, that, if the capital outlay be proportional to the weight of the metal in the cable, the most economical area of the conductor is that for which the annual interest on capital outlay equals the annual cost of the energy wasted in it.

A well-deserved tribute was paid to him when he was appointed, in 1890, to the chairmanship of the International Niagara Commission, which examined, reported on, and awarded prizes to plans for the generation and transmission of power from Niagara Falls. The commission finally selected for this great undertaking a system w r hich has since proved entirely successful; but not the least valuable part of its work w T as the collection and comparison of all the most recent information and practical results together with the best designs procurable in rope, hydraulic, pneumatic, and electric transmission. Lord Kelvin is associated with a smaller undertaking of the same nature nearer his home, the generation of power from the Falls of Foyer and its utilisation to manufacture aluminium by the British Aluminium Company.

The first Faure secondary batteries brought to Great Britain were submitted to him for testing, and his house at the university was the first in Great Britain to be lighted electrically, from top to bottom, by incandescent lamps. The whole installation was complete with its gas engine, batteries and shunt-wound dynamo and switches, automatic devices, and other instruments of his own design. In the earlier days of electricity supply companies and central stations Lord Kelvin’s aid was considered indispensable in every undertaking, and even to-day, when practice is more formulated, he is always busy with plans for some new scheme.

It may safely be said that no one has invented more or better electric measuring instruments for standard, laboratory, or commercial use. They are covered mainly by sixteen master patents, dating from 1881. Of the early instruments the graded and magnetostatic ammeters and voltmeters were based on the tangent galvanometer principle w r ith permanent controlling magnets. In the graded instruments provision was made for a long range, through which measurements could be made by moving the needle box and the controlling magnet to various distances along the axis of the coil.

In the magnetostatics, which are of the Helmholtz double-coil type, variations in the range and corrections for loss of magnetism in the magnets are permitted by the use of two sets of circular magnets which give a uniform field at the centre. One of the most important groups contain standard balances for both alternating and continuous currents, ampere balances to weigh from 1/100 up to 250 amperes, and watt balances suitable for currents up to 10,000 amperes. These are to be found in laboratories and stations all over the world, and a set has been supplied to the Board of Trade standardising laboratory.

The chief feature of this group of instruments lies in the fact that, as the outcome of ingenuity and good design, they permit the use of what is, undoubtedly, the most accurate method of measuring electric currents, — the weighing of the force between two coils; and combine convenience, accuracy, and rapidity, with absence of liability to derangement even when subjected to somewhat rough usage. In each instrument the mutual force, acting between fixed and movable coils carrying the current, is counterbalanced by moving a weight along a steelyard connected with the movable coils. The steelyard is suspended by filaments of fine copper wire which convey the current to the coils. Each instrument is provided with a set of weights, giving a wide range of readings and allowing the readings to be taken in the most sensitive part of the scale.

In many of Lord Kelvin’s voltmeters advantage is taken of the phenomena of electrostatic attractions and repulsions, and the instruments are thus suitable for both alternating and continuous circuits and free from temperature and iron errors. One group of electrostatic instruments, — the multicellular voltmeters, — form a series of standards between 30 and 2500 volts. Here the quadrant electrometer principle is modified to form a convenient commercial instrument. A number of thin, flat, aluminium, paddle-shaped needles are fixed horizontally at equal intervals on a fine platinum-iridium wire. These hang in spaces between two corresponding sets of insulated horizontal brass segments. A difference of potential existing between the segments and the needles draws them more underneath the corresponding segments against the action of the suspending wire; the deflection is read off on a scale, horizontal in the instruments intended for laboratory use, and vertical in the switchboard pattern. The same principle is applied in the vertical electrostatic voltmeters which are intended for higher voltages, — from 200 to 20,000 volts. There is only one needle, and it is suspended on knife edges so as to move in a vertical plane, the control being gravity.

The new dial electrostatic voltmeters are somewhat similar, but have a number of needles fixed on a spindle running in jewelled bearings. The control is gravity, and for convenience in central station work, the instruments are so arranged as to give a large open scale on each side of the normal voltage. The needle system balances at zero, but when displaced slightly an extra controlling weight is released. The lowest voltage for which the instrument is intended is just sufficient to counterbalance this, and the whole of the scale is thus available for readings within the prescribed limit.

For pressures up to 100,000 volts, the attracted disc principle is used in the electrostatic balance. A fixed plate attracts a movable disc, suspended from one end of a lever, the other end of which moves over a graduated scale. The Kelvin ampere and volt gauges are of the coil and plunger type, with gravity control and knife-edge bearings; the Kelvin central station voltmeters and recording voltmeters are constructed on the same principle. Another series of instruments, including voltmeters and wattmeters, are of the double-coil type, with gravity control and knife-edge bearings.

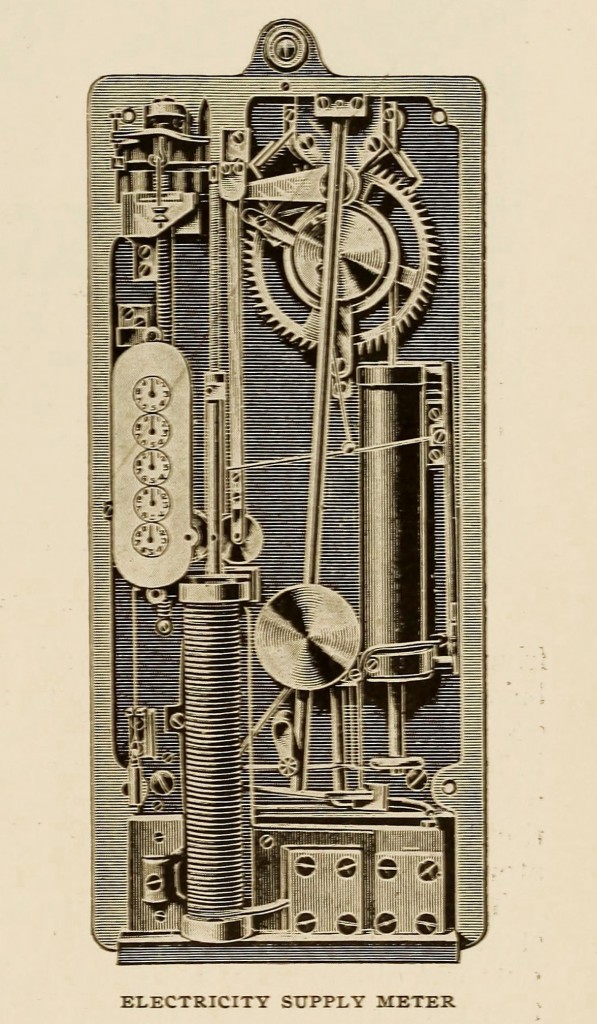
Lord Kelvin’s meters are of the periodic integrating coulomb meter type, — that is to say, the current consumed is not continuously added up, but samples are taken at short intervals of a few seconds and integrated, the current being assumed constant during the interval. The instrument consists of three parts, — the coil and plunger for measuring the current, the electrically- driven clock, and the integrating and recording gear. A soft iron plunger is supported inside a solenoid by a long spiral spring connected to one end of a small weighted lever supplied with an auxiliary spring. The adjustment of these is such that the deflection of the plunger is proportional to the current passing through the solenoid, even when the current is small. During each cycle the deflection is recorded by causing the plunger to move over the circumference of a friction wheel. This is the first of the recording train, and its motion is thus proportional to the quantity passing, the current being assumed constant during the cycle.

Pages might be filled with descriptions of numerous other instruments and various pieces of electrical apparatus invented by Lord Kelvin, including rheostats, volta piles, standard air condensers, an astronomical clock, and a water tap. A visit to Messrs. James White’s, a glance at the standardising laboratory where lane after lane is hedged with instruments of all kinds, getting the final touches, and a peep into the workshops where 250 men are all busy making apparatus devised by Lord Kelvin, impress one more than a detailed list with the extent and variety of his inventions. It was James White, the founder of the firm, philosophical instrument maker to the university, and thus a successor of James Watt, who constructed the first Kelvin instruments. He has long ago passed away, and there is now no White in the firm.

Lord Kelvin’s instruments are easily recognised. Simplicity in construction, ease of inspection and repair of the working parts, convenience in adjustment, geometrical guidance and constraint are all distinguishing features, and, needless to say, accuracy is an essential quality. In his early dealings with instrument makers Lord Kelvin found them possessed of a considerable amount of what he calls “mental inertia.” Many of his ideas, being quite opposed to existing practice, were looked upon with doubt; but they proved as successful as they were daring, and often the novelty, as well as the success, lay in the scientific design. One of his mottoes is, “Good workmanship cannot compensate for bad design.”

In many instruments we find examples of geometrical guidance and constraint, the principles of which are still comparatively unknown to instrument makers and engineers. Frequent use is made of his “hole, slot, and plane” arrangement, by means of which a piece of apparatus can be removed, returned to exactly the same position t and be quite free from stresses due to temperature or other expansions and contractions. Briefly, the apparatus is provided with three feet, perhaps levelling screws, with rounded ends. One goes into a three-sided pyramidal hole, another into a F-groove pointing to the hole, and the third rests on the plane itself. The apparatus and the body on which it rests may then be clamped together, if desired, by means of a spring, or a slightly elastic screw and nut. There is no space here for more than mere mention of Lord Kelvin’s contributions to the mathematical theories of electricity and magnetism, his long and extensive investigations on such subjects as contact electricity and atmospheric electricity and the wellknown resistance, capacity, insulation and other tests with which his name is associated.

The experiments by which he proved his prediction of the electrical convection of heat formed the starting-point of a series of investigations on the electrodynamic qualities of metals, the results of which were given in his Bakerian lecture to the Royal Society in 1856, and in further papers in 1875 and 1878. The eagerness with which he himself sought knowledge from experiments, and the enthusiasm which he imparted to his students, led, at the commencement of these investigations, to the establishment of his “volunteer laboratory corp” and the transformation of an unused wine cellar in the Old College into the first students’ physical laboratory in the world.

The constitution of matter and the size of atoms have always been subjects of great interest to him. In 1862 he showed, for the first time, how, from measurements in contact electricity, a limit could be given to the size of atoms, and afterwards, proceeding on four different lines of argument, founded on experimental results, he showed the very high degree of probability that, “in any ordinary liquid, transparent solid, or seemingly opaque solid, the mean distance between the centres of contiguous molecules is less than the one- five-millionth and greater than the one-one-millionth of a centimetre.”

To form some conception of the degree of coarse-grainedness indicated by this conclusion, imagine a globe of water or glass, as large as a football, to be magnified up to the size of the earth, each constituent molecule being magnified in the same proportion. The magnified structure would be more coarse-grained than a heap of small shot, but probably less coarse-grained than a heap of footballs.

Speculations and calculations regarding ether and the nature of electric and magnetic force have formed the substance of many papers. A few weeks after assuming the duties of his chair in 1846 he gave a “Mechanical Representation of Electric, Magnetic and Galvanic Forces,” which was published in the following year, and in 1890 he extended it so as to include magnetic induction. For this purpose, he assumed the ether to be incompressible and without elastic rigidity, but to have “a quasi rigidity depending on an inherent quasi elastic resistance to absolute rotation,” and he explained, in a paper given in the same year, “On a Gyrostatic Adynamic Constitution for ‘Ether,'” how such a medium could be realised mechanically.

As far back as 1854 he showed that, taking Pouillet’s data on solar radiation, the mechanical value of a cubic mile of sunlight is 12,050 foot-pounds; and estimated that a cubic mile of the luminiferous medium contains not less than 1-1060 of a millionth of a pound of matter.

He himself tells how these subjects have been uppermost in his mind for more than fifty years, and if it has not yet been permitted him to reach his goal and wrest from nature these profound secrets, at least his efforts have been noble, and through them many difficulties have been cleared away and the path has been made easier for further progress. It is touching to read the confession of failure that he made in an hour of triumph, — the celebration of his professorial jubilee:

“But when I think how infinitely little is all that I have done, I cannot feel pride; I see only the great kindness of my scientific comrades, and of all my friends, in crediting me for so much. One word characterises the most strenuous of the efforts for the advancement of science that I have made perseveringly during fifty-five years; that word is failure. I know no more of electric and magnetic force or of the relation between ether, electricity, and ponderable matter, or of chemical affinity than I knew and tried to teach to my students of natural philosophy fifty years ago in my first session as professor. Something of sadness must come of failure; but in the pursuit of science, inborn necessity to make the effort brings with it much of the certaminis gaudia, and saves the naturalist from being wholly miserable, — perhaps even allows him to be fairly happy, — in his daily work.”

Elasticity, hydrodynamics, the vortex theory, and all branches of mathematical physics have received numerous contributions from him, and pure mathematics has been enriched by many papers. In all, he has written about three hundred, but one does not marvel so much at the number as at their varied nature and comprehensiveness.

Many have been collected and form three volumes of mathematical and physical papers and one volume of papers on electrostatics and magnetism. There are, in addition, three volumes of popular lectures and addresses, and also the Baltimore lectures on “The Wave Theory of Light,” which he delivered in 1884 at Johns Hopkins University. Articles in “Nichol’s Cyclopaedia” and in the “Encyclopaedia Brittanica” have come from his pen.

One grand contribution which he gave, with Professor Tait, of Edinburgh, consists of the two volumes of the celebrated “Thomson and Tait’s Treatise on Natural Philosophy,” which appeared in 1867, and their “Elements of Natural Philosophy,” published in 1872. From 1846 to 1853 he was editor of the Cambridge Mathematical Journal, and for the past twenty-five years he has been a joint editor of the Philosophical Magazine.

Lord Kelvin’s writings are as easily recognised as his instruments. Even in his more mathematical papers there is an individuality of style. Accuracy in statement is a distinguishing characteristic, while in his popular lectures he constantly extracts information and illustration from commonplace things as well as from art, literature, and philosophy, both new and old. One of the presidents of the Royal Academy expressed his firm conviction that Lord Kelvin thinks in algebra. Sometimes when he comes to embody his conceptions in words, his hatred of ambiguity and love of strict accuracy in speech as well as in thought and the translation of mathematical formulae into words, lead to intricate and lengthy sentences (two hundred words is not uncommon) and the manufacture and introduction of words “not at present to be found in the dictionary.”

His scientific papers, however much they may bristle with mathematical expressions, are always brightened with some beautiful analogy or some practical application. Here lies the chief charm of his work as well as its outstanding feature. He has striven from the beginning to break down the barrier which existed between science and practice, to submit speculative science to experiment, and to base scientific theory on experimental facts. His own words express best his attitude and feelings on the relations between science and practice.

“There cannot,” he says, “be a greater mistake than that of looking superciliously upon the practical applications of science. The life and soul of science is its practical application, and just as the great advances in mathematics have been made through the desire of discovering the solution of problems which were of a highly practical kind in mathematical science, so in physical science many of the greatest advances that have been made from the beginning of the world to the present time have been made in the earnest desire to turn the knowledge of the properties of matter to some purpose useful to mankind.”

His influence on scientific thought and work during the latter half of the century springs not only from his publications, but from his teaching in the University of Glasgow; and scattered all over the world are men, now in the first rank of workers in natural philosophy, who can look back to the days when, in his classroom and laboratory, they first caught his inspiration and opened their eyes to scientific truths. His junior class usually consists of 200 students, — a heterogeneous collection preparing for all the professions, some
interested in the subject, some chiefly in examinations.

It is, perhaps, at the lecture table that Lord Kelvin displays most of his characteristics. In the two lectures per week, which he delivers to the junior class, he contrives to touch on most of the important points of his subject, passing from one to the other with a rapidity bewildering to lazy or ill-trained students who prefer the beaten track. On such members his digressions, often the most fascinating as well as the most valuable part of his lectures, are, alas, almost lost. His master mind, soaring high, sees one vast connected whole, and, alive with enthusiasm, with smiling face and sparkling eye, he shows the panorama to his pupils, pointing out the similarities and differences of its parts, the boundaries of our knowledge and the regions of doubt and speculation. To follow him in his flights is real mental exhilaration, a revelation and a keen delight to the better students, and the eyes of even the dullest lift at times from a seeming weary endless road and see the glory of the view.

He tests the students’ progress by weekly written examinations and by viva voce questions, which he passes from bench to bench during the progress of the lecture, following a practice which his father found so successful in teaching. The answering is not always satisfactory, and one morning, when the students were more than usually reticent in their replies, he wrote down on the blackboard the word “aphasia,” gave its Greek derivation, and defined it as “a virulent disease common among the students of the natural philosophy class.”

The elements of physical astronomy are included in the work of the class and voluntary reading set in it. Christmas vacations he considers a suitable time for reading, and once, to the students’ horror, he suggested that during it they should read a certain text-book of astronomy, pointing out that it could be got through at the rate of 50 pages per day. But this was quite to be expected from one to whom every moment is precious and has its own allotted work, and who, as a youth, contrived to master and expound Fourier’s “Analytical Theory of Heat” during the brief intervals of a fortnight’s travel on the continent.

Eggs, jellies, shoemaker’s wax, treacle, all sorts of stuff, are used to illustrate the lectures, and homely experiments are recommended to the student, even the humble teaspoon, “so ill adapted to the purpose for which it is intended,” being pressed into the service. In the famous egg experiment he shows how Columbus might have gained his object without breaking the egg. When boiled and set spinning on a table, the egg rises and spins on its end. Unboiled eggs, owing to the fluidity of the interior, do not rise, but if set spinning and then suddenly stopped and immediately released, they continue their motion for a little time. Once, the result of a students’ plot, raw eggs were substituted for the boiled ones, but science could discriminate, and the verdict was unhesitatingly given: — “None of them boiled.”

He revels in experiments, and is always at home and serenely happy, whether among forests of organ pipes and tuning forks, or in a sea of bottles and vessels for experiments on capillarity, or surrounded by globes and tops to illustrate astronomy. From the close of the prayer, with which, according to the ancient custom, the lecture is opened, until the end of the hour, his body as well as his mind is never at rest. With restless energy he will dart off to the blackboard to illustrate what he has been talking about, his gown streaming out behind him. Loud applause greets his efforts as he wrestles with gyrostats, or works energetically at the brake wheel to illustrate the principle of rope dynamometry.

The appearance of the ballistic pendulum is always hailed with delight by the class, for one of the classical experiments is to be performed, — the determination of the velocity of a bullet by firing it into the heavy wooden bob of the pendulum and noting the displacement produced. Armed with an old Jacob rifle with which, when a volunteer, he used to practice, Lord Kelvin comes to the front of the lecture table, kneels, takes deliberate aim, amid great amusement and excitement, pulls the trigger, and, before the smoke has subsided, is busy at the blackboard with the calculation.

His students are proud of him, admiring his energy and enthusiasm, respecting him for his profound knowledge and his grand work, loving him for his gentle, unassuming nature. On Graduation Day, 1891, after his appointment to the presidency of the Royal Society, they presented him with an illuminated address, amid a scene of the wildest enthusiasm. Many will long remember his claim to their fellowship, — “I have been a student of the University of Glasgow fifty-five years today, and I hope to continue a student of the university as long as I live.”

They thoroughly enjoy themselves at his “At Homes” for students. There he displays the great interest he takes in everything, even the most apparently trivial. With boyish delight he explains the latest puzzle or scientific toy, and shows lantern slides from which not even the comic element is excluded. On such occasions he is ably seconded by Lady Kelvin, and in this gracious hostess the students recognise one who, behind the scenes, has nobly done her work. How much the world owes to her assiduous care and helpfulness one cannot estimate; but she has proved, in the fullest, widest sense, a helpmate.

Lord Kelvin’s energy is wonderful, and undoubtedly his great physical strength is no negligible factor in the amount of work he has done. Unlike many other youthful prodigies, he can look back on a boyhood full of boyish sports, and on a youth when he enjoyed and graduated in the school of sports at Cambridge. In the early days of the volunteer movement he found time to devote to the duties of the service. Curling counted him among its devotees; but an unfortunate accident which befell him in a game, played more than thirty years ago, left him permanently lame and led to the severance of his connection with the volunteers. He humourously explains it: —

“It was this way, you know. I was all right standing at ease and at the manual exercise, but when it came to evolutions, the more the officer commanding ordered us to ‘march,’ the more I ‘halted.’ So I resigned.”

To-day in his seventy-sixth year he is fresh, vigorous, and working with the energy of youth. But in addition to a superb constitution, time is required for the performance of his multifarious work, teaching, experimenting, writing, lecturing, consulting, speaking in all parts of the country, scrupulously attending to duties, social functions and recreations. A keen politician, a fervid Unionist, he occupies his seat in the House of Lords whenever possible.

Perhaps mathematics has taught him the value of time infinitesimals. At all events, he integrates them. No moment is lost. Wherever he is, in quiet and peace, in scenes of hurry and bustle and noise, in the railway train or on a yachting cruise, whenever an idea strikes him, out comes one of the famous green note books and he is at once lost in thought and calculation. “Always carry a note-book, compasses, and a ruler,” is the “wrinkle” he gives his students.

In his house at the university you breathe an atmosphere of science. Everywhere you see portraits and souvenirs of the scientific giants of the century and their works, amid evidences of his own inventive genius, from the astronomical clock in the hall to the electric light apparatus and original systems of heating and ventilation. In the study you will find an early model of the perfected phonograph, and one of a pair of telephones brought over by Professor Bell to Great Britain. The other, connected to it by a private wire, is in the house of his nephew, James Thomson Bottomley, D. Sc, F. R. S., a few hundred yards away. Dr. Bottomley holds the post of Arnott and Thomson demonstrator in natural philosophy, and represents the Thomson family in the third successive generation that has supplied a teacher to the University of Glasgow. Himself a man of high and varied attainments and wide repute, he has, for more than twenty years, been associated with his uncle’s teaching and scientific work, and may justly be considered Lord Kelvin’s right-hand man.

A list of titles, degrees, diplomas, and other honours bestowed at different times on Lord Kelvin, would fill rather more than four pages of this magazine. In 1890, as Sir William Thomson, he was elected President of the Royal Society, a post once filled by Newton and now the honour of honours for the scientific men of Great Britain. A year afterwards he was raised to the peerage, with the title Baron Kelvin, of Largs, a distinction which, at the time, was unique in the annals of science. In 1896 he was appointed Knight of the Grand Cross of the Royal Victorian Order.

But his own country is not alone in acknowledging his genius. France has created him Grand Officer of the Legion of Honour; Germany, Knight of the Order pour le Merite; and Belgium, Commander of the Order of Leopold. Four times he has been president of the Royal Society of Edinburgh, and twice president of the Institution of Electrical Engineers. The British Association, with which he has long been connected and in whose affairs he takes a warm and ceaseless interest, elected him as president of its Edinburgh meeting in 1871. The Institut de France has awarded him the Prix Poncelet, and bestowed on him the almost unique distinctions of Foreign Associate and Arago Medallist. He has been awarded the Copley and Royal Medals of the Royal Society, the Keith Medal of the Royal Society of Edinburgh, and the Helmholtz Medal.

He is an honorary member of most of the important scientific societies in the world. Fourteen universities have conferred on him the degree of Honorary Doctor, of civil law, of laws, of science, of physical science, of philosophy, and of natural philosophy. In 1884 the University of Heidelberg, at its tercentenary celebrations, desiring to confer an honorary degree on him, and finding that the only one at their disposal which he did not already possess was that of Doctor of Medicine, accordingly presented him with that diploma. On the very day on which it arrived his kindly eye noticed the indisposition of his lecture-room assistant, and thereupon he wrote out his first prescription, in proper language and form. Nature was the remedy, and a week the dose. His possession of the degree of M. D. led to an amusing scene a few years ago when giving evidence in a famous medical electric case. An opposing counsel, desiring to make a point, remarked that he presumed Lord Kelvin’s numerous qualifications did not include those of a doctor of medicine; and one may imagine his confusion when Lord Kelvin ingenuously replied that he had received the degree of M. D. from Heidelberg University.

Such honours, conferred on Lord Kelvin, enable one to judge how highly he is everywhere esteemed; but even they fall short of that which was given in 1896, when, from every civilised country, from every corner of the globe, came students, professors and representatives of scientific societies, bearing honours and congratulations, to take part in the celebration of his jubilee as a professor at Glasgow University. Never before had such a distinguished company of scientific men been gathered together, and the enthusiastic and impressive proceedings will long be remembered by those who took part in them. Cables carried congratulatory messages over every ocean, and delivered them to the siphon recorders which were on exhibition with Lord Kelvin’s other inventions. It was a stirring and a hopeful scene. Men of all nations, bound by one tie, united to do honour to one man whom they all claimed as brother.

It is difficult to realise that we have among us to-day, active and productive as ever, one who has marched in the van of scientific progress for more than fifty years. To-day, in his seventy-sixth year, he is still young and working with unabated energy and success. Surely we may say of him, as he said of Joule, “It was hard work, early begun and persevered in, and conscientiously carried out; that is the foundation of all great works, whether in literature, philosophy or science, or in doing good to the world in any possible way.”

In his work there is manifest the genius that has the capacity for taking infinite pains as well as the genius that does great things seemingly without effort. Such an intellect is like the farseeing telescope which, when reversed, becomes a microscope. Nothing is too large; nothing too small. Everything is subject to scrutiny. Who that has heard of him does not admire his grand work and his tireless genius? Who that knows him does not love his simple, happy nature? Surely we join the cry: — “Long live Lord Kelvin.”